Dark matter

distribution, structure and content in galaxies

Introduction
The ‘diversity’ of dwarf galaxy rotation curves

Introduction

My main line of research focuses on the dark matter content and structure in galaxies. I first became interested in dark matter as a research topic (beyond the level of ‘dark matter - that sounds cool!’) as a senior undergraduate when the various parametrizations (NFW, Einasto, …) of dark matter density profiles came up in lecture. I remember wondering how we could possibly have such a detailed understanding of the distribution of something so little understood.

A map of the dark matter density (left) and atomic gas density (right) in a simulated dwarf galaxy from a development version of the COLIBRE galaxy formation model. Velocity vectors of a subset of the gas particles are shown with arrows in the right panel. The gas is in a rotationally-supported disc, but perturbed by supernova explosions that have opened up the bubbles visible in the disc - these also clearly perturb the velocity field.

My starting point

I picked up some more background knowledge while doing my MSc in satellite galaxy evolution, enough that once I was accepted to the PhD programme in Victoria and got round to picking a project I proposed to work on the cusp-core problem supervised by Julio Navarro. This ‘problem’ was at the time a statement of the fact that simulations of dark matter evolving under the influence of gravity forms clumps (‘halos’) that get denser towards their centres with a power law slope of about -1, while observations of some galaxies are more consistent with a central region of constant dark matter density (power law slope of 0). The original papers on the subject go back to the mid-nineties, so this was not a newly identified discrepancy. Right around the same time there were some major advances in simulations that soon culminated in the EAGLE simulations and the many associated spinoff projects, including the APOSTLE project (Sawala et al. 2016) that I was heavily involved in. Rotation curves of galaxies from the THINGS and especially the LITTLE THINGS 21‑cm radio surveys surveys were also being published around the same time. This combination of circumstances offered an opportunity to make some new contributions on the subject.

Dwarf galaxies

Dwarf galaxies typically have low stellar and gas densities, low enough that even in there centres the dark matter density can be higher than the visible matter density. Since the dark matter is then the main contributor to the gravitational potential, dwarf galaxies make good targets for study since the dark matter ‘signal’ is high relative to the visible matter ‘noise’.

Rotation curves

One way to measure the dark matter content and distribution in a galaxy is with a rotation curve. In the simplest case, the speed \(v\) of a particle on a circular orbit of radius \(r\) in a spherically-symmetric gravitational potential is related to the mass enclosed within the orbit \(M(<r)\) as \(v(r)=\sqrt{GM(<r)/r}\). If we can measure the orbital speeds of “tracer” particles at a series of radii to build up the rotation curve \(v(r)\), we directly get the mass profile \(M(<r)\). If we subtract off the mass profile of the visible matter (stars, gas) we’re left with the dark matter mass profile.

In realistic galaxies there are some complications:

the gravitational potential is probably not spherically symmetric (but if the mass budget is dominated by dark matter it might be a reasonable approximation);
the “tracer” particles are probably not all on circular orbits;
with the exception of the Milky Way and galaxies in its immediate vicinity, we only measure angular positions and velocities along the line of sight, so we have incomplete information;
gravity may not be the only force acting.

Nevertheless, in some cases these complications can be modelled or neglected and the general approach still works.

21‑cm, radio or ‘HI’ emission from atomic hydrogen is perhaps the best-known spectral line used to measure rotation curves. The atomic gas has the advantage of often extending well beyond the stellar disc, allowing measurements to larger radii, and the emission physics and radiative transfer are quite simple, making it relatively easy to model.

The ‘diversity’ of dwarf galaxy rotation curves

When I started working on the cusp-core problem the conversation in the literature centred around the slope of the dark matter density profile measured at as small a radius as possible. This has some drawbacks, chiefly that the ‘figure of merit’ (that slope) is very far from what is actually measured (a rotation curve, at least at the first-derived-data-product level). To get from a rotation curve to a density profile first the rotation curve needs to be interpreted as a mass profile (with some uncertainty). Then a derivative needs to be taken to get a density profile, followed by a second derivative to measure its slope. Pushing to the smallest possible radius makes this even more challenging, as does the fact that the dark matter density profile is usually thought of in log-density and log-radius, while the rotation curve is sampled linearly in radius. One of the main goals of my first paper (Oman et al. 2015) on the topic was to propose a formulation of the cusp-core problem that is much more directly anchored in what is actually measured. Comparing the amplitude of the rotation curve at an ‘inner’ and an ‘outer’ radius turns out to do the job, as summarised in Fig. 5 of the paper:

Rotation curves of four dwarf irregular galaxies of approximately the same maximum rotation speed V_max (80-100 km s^-1) and galaxy mass, chosen to illustrate the diversity of rotation curve shapes at given V_max. Coloured solid curves and shaded areas correspond to the median (and 10^th-90^th percentile) circular velocity curve of simulated galaxies matching (within 10 per cent) the maximum circular velocity of each galaxy. Note that the observed rotation curves exhibit a much wider diversity than seen in the simulations, from galaxies like UGC 5721, which are consistent with our simulations, to galaxies like IC 2574, which show a much more slowly-rising rotation curve compared with simulations, either hydrodynamical (coloured lines) or dark matter-only (black lines).

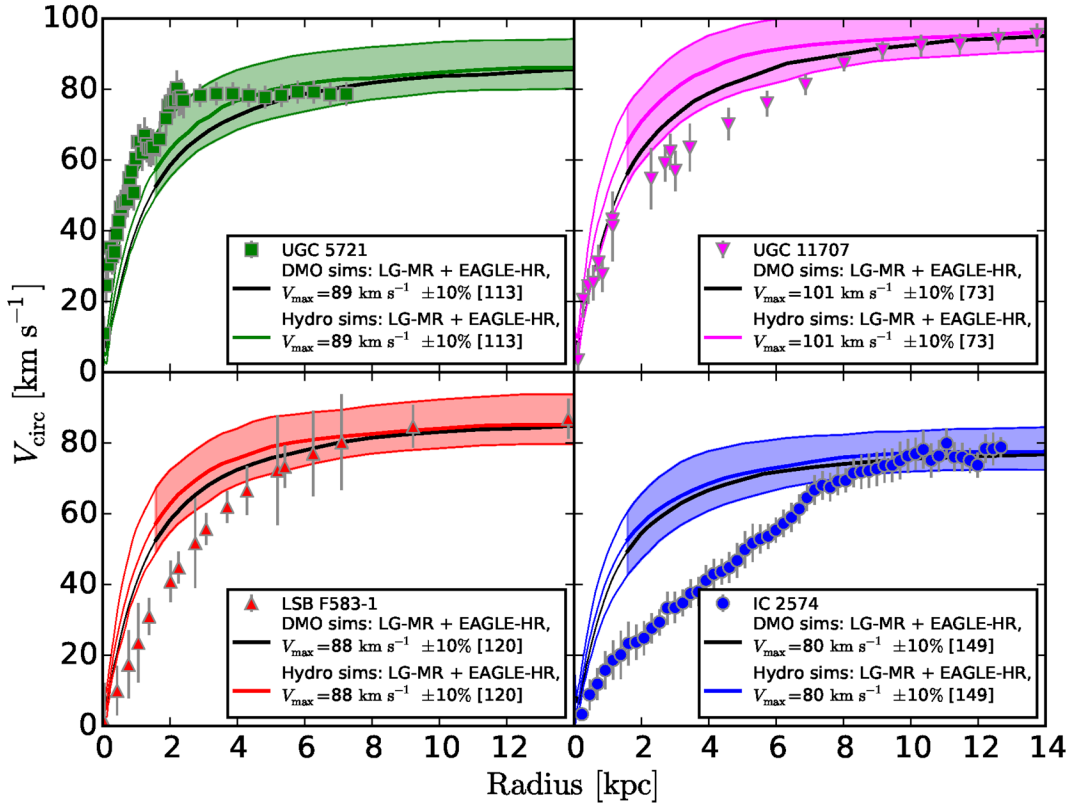
Since the four galaxies have a fixed V_max, the shapes of their rotation curves can be parametrised with one number, the amplitude at an inner radius. In this initial paper we used 2 kpc, but later (Santos-Santos et al. 2020) refined our definition so that the ‘inner’ radius scales with the size of the galaxy, leading to a figure that had a lot of influence in the field (this version from the later paper’s Fig. 2):

Rotation speed at the inner radius V_fid versus maximum rotation speed for all galaxies in our observational sample. Galaxies with rapidly-rising rotation curves lie near the 1:1 dotted line. Rotation curves with (V_fid, V_max) values consistent with dark matter-only ΛCDM halos lie along the grey curve and shaded area, computed using the median M₂₀₀(c) relation (plus 10-90 and 1-99 percentiles) for a Planck-normalized cosmology. Slowly-rising rotation curves (i.e. 'cored' galaxies with a substantial inner mass deficit relative to ΛCDM) lie below the grey-shaded area. Each galaxy is labelled with its name and coloured according to η_rot, which we adopt as a simple measure of rotation curve shape.

The ‘diversity’ from the title of the paper refers to the vertical scatter for galaxies with V_max between about 50 and 150 km s^-1 - typically these are dwarf irregular (dIrr) or low-surface brightness (LSB) galaxies. The usefulness of this figure comes from the fact that the quantities plotted on the axes are much closer to what is directly measured than other attempts to express something similar in terms of the slope of the dark matter density profile, for example. It should not, however, be considered in isolation. It is true that dIrr and LSB galaxies exhibit diversity in their central matter content at fixed dynamical mass, as the figure shows, but it is not random. I’ve been asked before how it can be that the rotation curves of low-mass galaxies have diverse shapes, yet can give rise to the radial acceleration relation (RAR), that strongly suggests uniformity rather than diversity. Part of the answer is that the shapes of the rotation curves correlate strongly with some properties of galaxies, notably their surface brightnesses (or surface densities if gas is included, or other related metrics). The total matter surface density seems to correlate, perhaps more strongly than we’d expect, with the visible matter surface density. Expressing things in terms of surface densities, as the RAR essentially does, highlights this in a way that the V_fid vs. V_max figure does not.

Explaining the diversity in rotation curve shapes

Another point that we (Oman et al. 2015) emphasized is that there are a limited number of ways that the diversity in low-mass galaxy rotation curve shapes can be explained. The comprehensive list has only 4 items:

Dark matter could be re-distributed away from a cuspy distribution by the physics of normal matter, such as by the gravitational influence of gas flows driven by repeated cycles of gas cooling and supernova-driven winds.
Dark matter could be re-distributed away from a cuspy distribution by the physics of dark matter, such as by a collisional interaction between pairs of dark matter particles.
Our interpretation of the measurements may be incorrect because we have assumed the wrong gravitational force law (i.e. we could consider alternatives such as modified Newtonian dynamics).
Our interpretation of the measurements may be incorrect because we have made flawed assumptions in modelling the data.

Much of my work since has been focused on the last point as a possible explanation. I am at this point convinced that there are systematic errors in the modelling and interpretation of the rotation of low-mass galaxies at a level that cannot be ignored. That these would be enough to completely resolve the cusp-core debate by making every galaxy consistent with hosting a dark matter cusp if they were corrected, however, seems like a stretch. My view is therefore that we need to clean up the modelling to know what we should be aiming for more broadly with galaxy formation models (like: how much do we need stellar feedback to reshape the dark matter distribution in galaxies?).

I think that much of the systematic error budget in modelling the gas kinematics in low-mass galaxies can be assigned to mismatches between the assumptions made in the models and reality. A straightforward example is that the classical ‘tilted-ring’ approach assumes that at any given radius the gas is axisymmetric, with no modulation in velocity around the ring. This is essentially guaranteed to be false at some level, and our work (Oman et al. 2019) with simulated galaxies suggests that gas in roughly elliptical orbits (rather than circular) could realistically drive a lot of the scatter in rotation curve shapes. A clear example of such elongated orbits is illustrated in that paper’s Fig. 6:

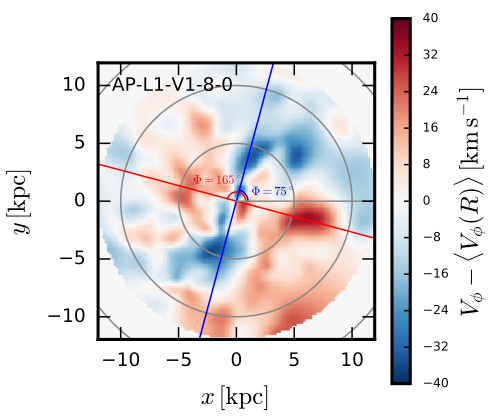
Face-on map of the residual azimuthal motions (after subtracting the mean rotation as a function of radius) in the disc plane for a dwarf irregular galaxy from the APOSTLE simulation suite. The red and blue lines correspond to the directions that approximately lie along the principal axes of the bisymmetric (m=2) pattern in the residual velocity field. They grey circles are drawn at intervals of 5 kpc.

The elongation of the gas orbits is probably driven by an elongated shape of the dark matter halos in which they are embedded (Marasco et al. 2018). A similar argument applies to the assumption that the gas disc is geometrically thin, when in fact it is likely thick enough that any given sight line through an inclined disc passes through several of the rings that it is decomposed into in a model.

We (Oman et al. 2019) summarized the cumulative effects of gas being perturbed so that it doesn’t quite rotate at the circular velocity (V_ϕ compared to V_circ) and then of systematic errors in modelling the gas kinematics (modeled mock observations compared to V_ϕ) in the same space of inner rotation velocity versus maximum rotation velocity explained above. The initially tightly clustered circular velocity curve shapes (from V_circ, red points) end up looking much more like the observed distribution (blue points) once they are “observed” and modelled (black points) in the same way as the observations (from the paper’s Fig. 9):

Circular velocity at 2 kpc plotted against maximum circular velocity, a measure of the 'central mass deficit'. The lines are reproduced from fig. 6 of Oman et al. (2015). The solid black line indicates the expected correlation for an NFW mass profile and the mass concentration relation of Ludlow et al. (2014); this is well traced by halos in dark-matter-only versions of the APOSTLE and EAGLE simulations. Values measured from the circular velocity profiles of galaxies from the (hydrodynamical) APOSTLE and EAGLE simulations lie along the red line. The broken lines indicate the correlation for the same (NFW) profile but removing a fixed amount of mass from the central 2 kpc, as labelled. Three points are shown for each of the APOSTLE galaxies in our sample: one for the circular velocity at 2 kpc (red), another for the gas azimuthal speed corrected for pressure support (green), and a third for the ^3DBAROLO estimates of the rotation speed corrected for pressure support (black). Each quantity as shown as a function of the maximum of the circular velocity of each system, V_max. We show measurements from the THINGS (blue diamonds) and LITTLE THINGS (blue squares) surveys for comparison.

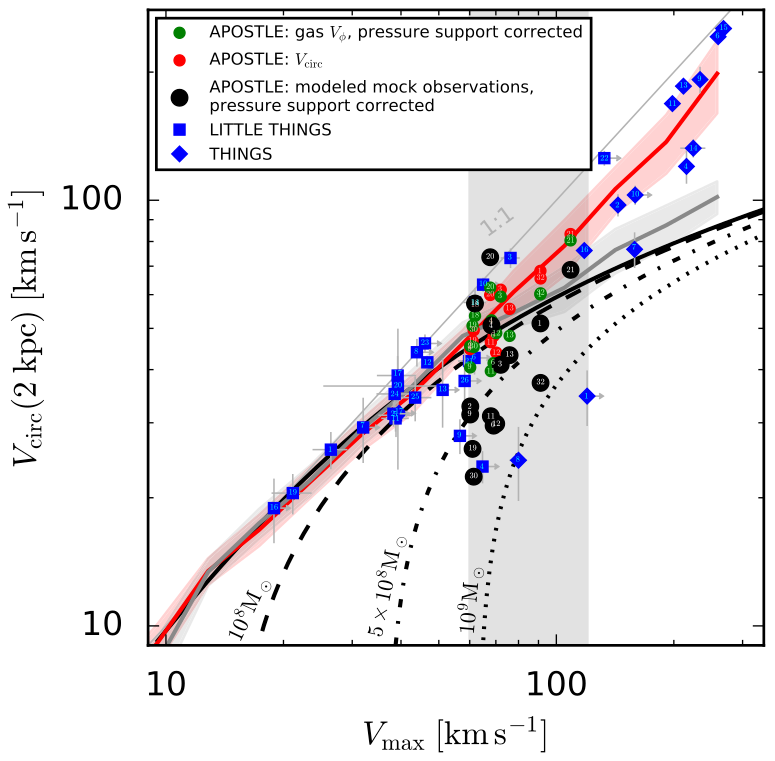
Further hints to the origin of the diversity in rotation curve shapes

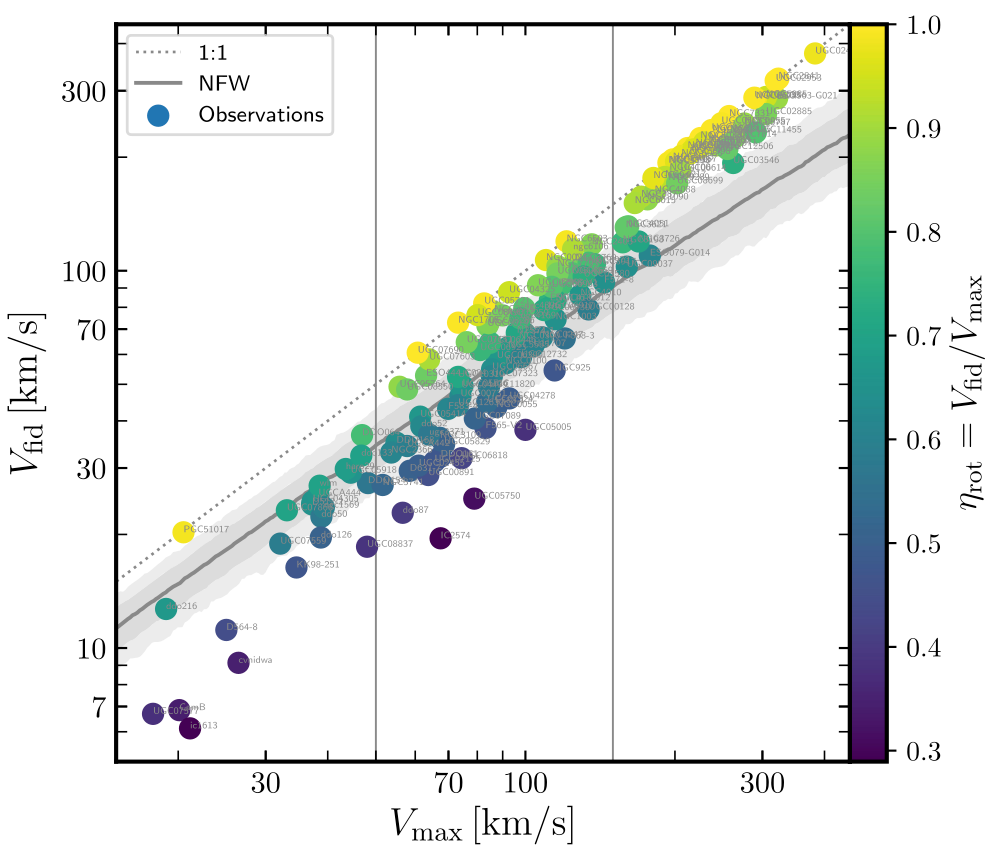
The next significant development that I was involved in (Santos-Santos et al. 2020) was the development of a somewhat compressed version of the rotation curve shape plot (V_fid vs V_max or V_(2 kpc) vs V_max) so that information about the dynamical importance of the dark matter could also be included. The y-axis shows a parameter η_rot=V_fid/V_max that summarises how steeply-rising the rotation curve is, while the x-axis shows η_bar, that is approximately equal to the ratio of baryonic-to-total mass in the central regions of a galaxy. (This version taken from Fig. 4 of the paper.)

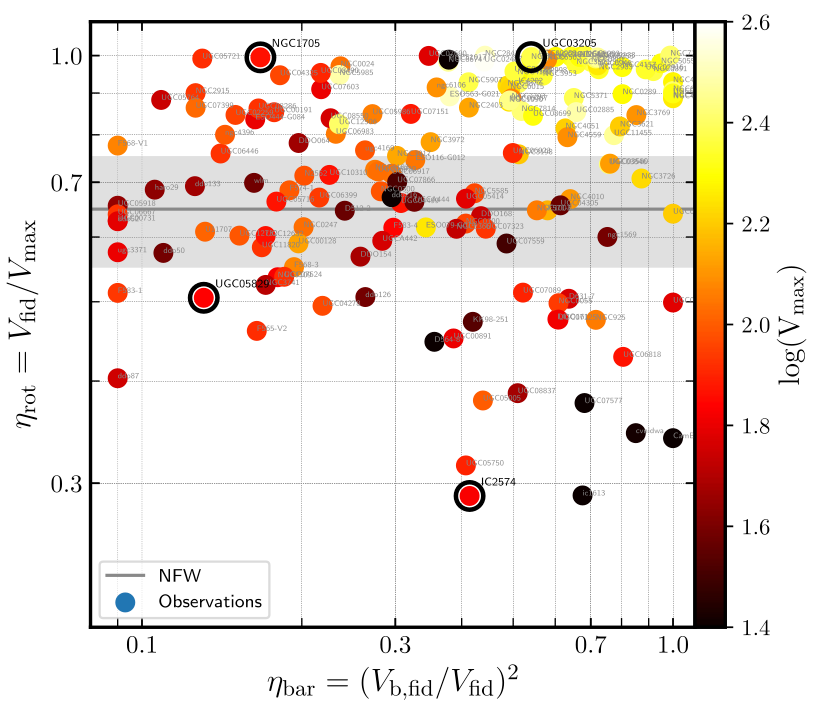
Rotation curve shape parameter, η_rot, as a function of the gravitational importance of the baryonic component at the inner fiducial radius, η_bar, for a sample of observed galaxies. The latter is approximately the ratio between baryonic and total enclosed masses withing r_fid. Galaxies are coloured by maximum circular velocity, as indicated by the colourbar. Dark matter-only ΛCDM halos have, on average, η_rot ~0.65, with 10:90 percentile scatter as indicated by the grey band. Systems with η_bar<0.09 are shown at that value for clarity.

The distribution of low-mass galaxies (orange to black on the colour bar) in this space turns out to be very informative. The trend runs from the upper left of the figure to the lower right, with plenty of scatter. In words, this means that the most centrally ‘dark matter-dominated’ galaxies have the steeply-rising rotation curves associated with dark matter cusps, while centrally baryon-dominated galaxies have slowly-rising rotation curves associated with dark matter cores. In some contexts this could be intuitive. For example, if we hypothesize that cores are created by re-distribution of dark matter following episodes supernova-driven winds, then it makes sense that having a high enough baryon density in the centre of the galaxy to have a significant dynamical influence on the dark matter would be a pre-requisite. As we went through in detail in the paper, however, no simulation or similar model at the time could satisfactorily reproduce the observed trend (and to my knowledge this hasn’t changed since, with the possible exception of the New Horizon simulations). It turns out, however, that the types of systematic errors that come up when trying to model the gas kinematics in these kinds of galaxies, like those due to non-circular gas orbits mentioned above, naturally lead to the observed trend and scatter. To me this is another hint that such modelling errors are the leading effect that we’re seeing in observational studies, but doesn’t rule out that there might be signatures of interesting physics like cores created by supernova feedback or dark matter scattering interactions to be found once the models are cleaned up.

Supernova feedback-driven dark matter cores as an explanation

My MPhys student Finn Roper’s project (Roper et al. 2023) looked at whether once simulated galaxies are observed at 21‑cm wavelengths and modelled analogously to what is done with real galaxies we could still tell the difference between galaxies with a dark matter cusp and others with dark matter cores. The η_rot-η_bar figure introduced above makes a good diagnostic for this (taken from the paper’s Fig. 11):

Rotation curve shape parameter, η_rot, as a function of central baryon-to-total mass fraction η_bar. The solid black line shows the average η_rot expected for NFW cusps and the grey band shwos corresponding 10-90 per cent scatter. Upper panel: the square symbols are measured from the circular velocity curves (derived from the gravitational acceleration field in the disc mid-plane) of 21 simulated galaxies with a low gas density threshold (LT) for star formation. For each galaxy, there are 24 points for measurements derived from 24 rotation curves, one for each of 24 sightlines used to mock-observe each of them, with one orientation for each galaxy corresponding to the points outlined in black. These give an impression of the range in rotation curve shapes which might be measured given the intrinsic shapes reflected by the square markers. Darker and lighter error bars show median fractional uncertainties for galaxy subsamples with V_max<75 km s^-1 and V_max>75 km s^-1, respectively. Crosses show measurements derived from rotation curves of a selectoin of observed galaxies. Lower panel: as upper panel, but for 11 simulated galaxies with a high gas density threshold (HT) for star formation. Even though the circular velocity curves (square markers) lie in a distinct region of this parameter space relative to the LT galaxies, once the 'observational scatter' is included (points), the distributions overlap much more.

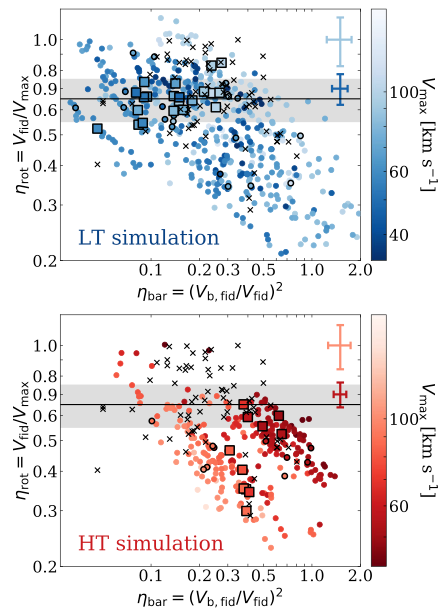
The galaxies in the upper panel all have dark matter cusps, while most of those in the lower panel have cores formed by repeated cycles of gas accretion and ejection by supernova winds. This manifests as a vertical offset between the square markers, which reflect the intrinsic matter distribution in the galaxies. There’s also a horizontal offset, showing that the galaxies that form cores tend to have somewhat higher baryon-to-dark matter ratios in their centres. This turns out to be a combination of less dark matter (due to the core) and more baryons, particularly in the portion of the cycle just before a burst of supernovae. Once the galaxies are observed (24 observations per galaxy, shown with the small points) in both cases the measurements scatter significantly along the upper left-to-lower right diagonal. There’s a preference to scatter towards the bottom right because of errors induced by the thickness of the discs; this is less pronounced in the cored galaxies where the discs tend to be thinner. In the end the two distribution overlap substantially. If I squint at the figure for long enough, maybe the galaxies with dark matter cusps resemble the observations (black crosses) slightly more than the galaxies with cores, but there are a lot of sample selection issues to worry about before trying to make that kind of claim in a convincing way. The way that we got galaxies to make dark matter cores also involves quite a blunt instrument - we just turned up the gas density threshold for star formation in the EAGLE galaxy formation model. There’s definitely some room for further work with other models that produce galaxies with dark matter cores without arbitrarily changing model parameters, or perhaps to vary a model to cover both cases but re-calibrate it so that the comparison is between the ‘best’ model in both scenarios. Nonetheless, this work highlights again that modelling uncertainties are really the first hurdle to overcome when interpreting observations of these kinds of galaxies to get at their dark matter content and distribution.

References

2023

The many reasons that the rotation curves of low-mass galaxies can fail as tracers of their matter distributions

Eleanor R. Downing, and Kyle A. Oman

(2023) MNRAS 522 3318

Abs ADS arXiv Bib HTML PDF

It is routinely assumed that galaxy rotation curves are equal to their circular velocity curves (modulo some corrections) such that they are good dynamical mass tracers. We take a visualization- driven approach to exploring the limits of the validity of this assumption for a sample of 33 low-mass galaxies (60 v_max/km s^-1 120) from the APOSTLE suite of cosmological hydrodynamical simulations. Only three of these have rotation curves nearly equal to their circular velocity curves at z = 0, the rest are undergoing a wide variety of dynamical perturbations. We use our visualizations to guide an assessment of how many galaxies are likely to be strongly perturbed by processes in several categories: mergers/interactions (affecting 6/33 galaxies), bulk radial gas inflows (19/33), vertical gas outflows (15/33), distortions driven by a non-spherical DM halo (17/33), warps (8/33), and winds due to motion through the intergalactic medium (5/33). Most galaxies fall into more than one of these categories; only 5/33 are not in any of them. The sum of these effects leads to an underestimation of the low-velocity slope of the baryonic Tully-Fisher relation (α ∼3.1 instead of α ∼3.9, where M_bar ∝ v^α) that is difficult to avoid, and could plausibly be the source of a significant portion of the observed diversity in low-mass galaxy rotation curve shapes.
@article{2023MNRAS.522.3318D, author = {{Downing}, Eleanor R. and {Oman}, Kyle A.}, title = {{The many reasons that the rotation curves of low-mass galaxies can fail as tracers of their matter distributions}}, journal = {\mnras}, keywords = {galaxies: dwarf, galaxies: kinematics and dynamics, dark matter, Astrophysics - Astrophysics of Galaxies}, year = {2023}, month = jul, volume = {522}, number = {3}, pages = {3318-3336}, doi = {10.1093/mnras/stad868}, archiveprefix = {arXiv}, eprint = {2301.05242}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2023MNRAS.522.3318D}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }
The diversity of rotation curves of simulated galaxies with cusps and cores

Finn A. Roper, Kyle A. Oman, Carlos S. Frenk, and 3 more authors

(2023) MNRAS 521 1316

Abs ADS arXiv Bib HTML PDF

We use ΛCDM cosmological hydrodynamical simulations to explore the kinematics of gaseous discs in late-type dwarf galaxies. We create high-resolution 21-cm ’observations’ of simulated dwarfs produced in two variations of the EAGLE galaxy formation model: one where supernova-driven gas flows redistribute dark matter and form constant-density central ’cores’, and another where the central ’cusps’ survive intact. We ’observe’ each galaxy along multiple sightlines and derive a rotation curve for each observation using a conventional tilted- ring approach to model the gas kinematics. We find that the modelling process introduces systematic discrepancies between the recovered rotation curve and the actual circular velocity curve driven primarily by (i) non-circular gas orbits within the discs; (ii) the finite thickness of gaseous discs, which leads to overlap of different radii in projection; and (iii) departures from dynamical equilibrium. Dwarfs with dark matter cusps often appear to have a core, whilst the inverse error is less common. These effects naturally reproduce an observed trend which other models struggle to explain: late-type dwarfs with more steeply rising rotation curves appear to be dark matter- dominated in the inner regions, whereas the opposite seems to hold in galaxies with core-like rotation curves. We conclude that if similar effects affect the rotation curves of observed dwarfs, a late-type dwarf population in which all galaxies have sizeable dark matter cores is most likely incompatible with current measurements.
@article{2023MNRAS.521.1316R, author = {{Roper}, Finn A. and {Oman}, Kyle A. and {Frenk}, Carlos S. and {Ben{\'\i}tez-Llambay}, Alejandro and {Navarro}, Julio F. and {Santos-Santos}, Isabel M. E.}, title = {{The diversity of rotation curves of simulated galaxies with cusps and cores}}, journal = {\mnras}, keywords = {galaxies: dwarf, galaxies: kinematics and dynamics, dark matter, Astrophysics - Astrophysics of Galaxies}, year = {2023}, month = may, volume = {521}, number = {1}, pages = {1316-1336}, doi = {10.1093/mnras/stad549}, archiveprefix = {arXiv}, eprint = {2203.16652}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2023MNRAS.521.1316R}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }

2020

Baryonic clues to the puzzling diversity of dwarf galaxy rotation curves

Isabel M. E. Santos-Santos, Julio F. Navarro, Andrew Robertson, and 7 more authors

(2020) MNRAS 495 58

Abs ADS arXiv Bib HTML PDF

We use a compilation of disc galaxy rotation curves to assess the role of the luminous component (’baryons’) in the rotation curve diversity problem. As in earlier work, we find that rotation curve shape correlates with baryonic surface density: high surface density galaxies have rapidly rising rotation curves consistent with cuspy cold dark matter haloes; slowly rising rotation curves (characteristic of galaxies with inner mass deficits or ’cores’) occur only in low surface density galaxies. The correlation, however, seems too weak to be the main driver of the diversity. In addition, dwarf galaxies exhibit a clear trend, from ’cuspy’ systems where baryons are unimportant in the inner mass budget to ’cored’ galaxies where baryons actually dominate. This trend constrains the various scenarios proposed to explain the diversity, such as (I) baryonic inflows and outflows during galaxy formation; (II) dark matter self- interactions; (III) variations in the baryonic mass structure coupled to rotation velocities through the ’mass discrepancy- acceleration relation’ (MDAR); or (IV) non-circular motions in gaseous discs. Together with analytical modelling and cosmological hydrodynamical simulations, our analysis shows that each of these scenarios has promising features, but none seems to fully account for the observed diversity. The MDAR, in particular, is inconsistent with the observed trend between rotation curve shape and baryonic importance; either the trend is caused by systematic errors in the data or the MDAR does not apply. The origin of the dwarf galaxy rotation curve diversity and its relation to the structure of cold dark matter haloes remains an open issue.
@article{2020MNRAS.495...58S, author = {{Santos-Santos}, Isabel M. E. and {Navarro}, Julio F. and {Robertson}, Andrew and {Ben{\'\i}tez-Llambay}, Alejandro and {Oman}, Kyle A. and {Lovell}, Mark R. and {Frenk}, Carlos S. and {Ludlow}, Aaron D. and {Fattahi}, Azadeh and {Ritz}, Adam}, title = {{Baryonic clues to the puzzling diversity of dwarf galaxy rotation curves}}, journal = {\mnras}, keywords = {galaxies: dwarf, galaxies: evolution, galaxies: formation, galaxies: haloes, dark matter, cosmology: theory, Astrophysics - Astrophysics of Galaxies}, year = {2020}, month = jun, volume = {495}, number = {1}, pages = {58-77}, doi = {10.1093/mnras/staa1072}, archiveprefix = {arXiv}, eprint = {1911.09116}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2020MNRAS.495...58S}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }

2019

Non-circular motions and the diversity of dwarf galaxy rotation curves

Kyle A. Oman, Antonino Marasco, Julio F. Navarro, and 3 more authors

(2019) MNRAS 482 821

Abs ADS arXiv Bib HTML PDF

We use mock interferometric HI measurements and a conventional tilted- ring modelling procedure to estimate circular velocity curves of dwarf galaxy discs from the APOSTLE suite of Λ cold dark matter cosmological hydrodynamical simulations. The modelling yields a large diversity of rotation curves for an individual galaxy at fixed inclination, depending on the line-of-sight orientation. The diversity is driven by non-circular motions in the gas; in particular, by strong bisymmetric fluctuations in the azimuthal velocities that the tilted-ring model is ill-suited to account for and that are difficult to detect in model residuals. Large misestimates of the circular velocity arise when the kinematic major axis coincides with the extrema of the fluctuation pattern, in some cases mimicking the presence of kiloparsec- scale density ‘cores’, when none are actually present. The thickness of APOSTLE discs compounds this effect: more slowly rotating extra-planar gas systematically reduces the average line-of-sight speeds. The recovered rotation curves thus tend to underestimate the true circular velocity of APOSTLE galaxies in the inner regions. Non-circular motions provide an appealing explanation for the large apparent cores observed in galaxies such as DDO 47 and DDO 87, where the model residuals suggest that such motions might have affected estimates of the inner circular velocities. Although residuals from tilted-ring models in the simulations appear larger than in observed galaxies, our results suggest that non-circular motions should be carefully taken into account when considering the evidence for dark matter cores in individual galaxies.
@article{2019MNRAS.482..821O, author = {{Oman}, Kyle A. and {Marasco}, Antonino and {Navarro}, Julio F. and {Frenk}, Carlos S. and {Schaye}, Joop and {Ben{\'\i}tez-Llambay}, Alejandro}, title = {{Non-circular motions and the diversity of dwarf galaxy rotation curves}}, journal = {\mnras}, keywords = {ISM: kinematics and dynamics, galaxies: haloes, galaxies: structure, dark matter, Astrophysics - Astrophysics of Galaxies, Astrophysics - Cosmology and Nongalactic Astrophysics}, year = {2019}, month = jan, volume = {482}, number = {1}, pages = {821-847}, doi = {10.1093/mnras/sty2687}, archiveprefix = {arXiv}, eprint = {1706.07478}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2019MNRAS.482..821O}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }

2018

Bars in dark-matter-dominated dwarf galaxy discs

A. Marasco, K. A. Oman, J. F. Navarro, and 2 more authors

(2018) MNRAS 476 2168

Abs ADS arXiv Bib HTML PDF

We study the shape and kinematics of simulated dwarf galaxy discs in the APOSTLE suite of Λ cold dark matter (ΛCDM) cosmological hydrodynamical simulations. We find that a large fraction of these gas-rich, star-forming discs show weak bars in their stellar component, despite being dark-matter-dominated systems. The bar pattern shape and orientation reflect the ellipticity of the dark matter potential, and its rotation is locked to the slow figure rotation of the triaxial dark halo. The bar-like nature of the potential induces non-circular motions in the gas component, including strong bisymmetric flows that can be readily seen as m = 3 harmonic perturbations in the HI line-of-sight velocity fields. Similar bisymmetric flows are seen in many galaxies of The HI Nearby Galaxy Survey (THINGS) and Local Irregulars That Trace Luminosity Extremes THINGS (LITTLE THINGS), although on average their amplitudes are a factor of ∼2 weaker than in our simulated discs. Our results indicate that bar-like patterns may arise even when baryons are not dominant, and that they are common enough to warrant careful consideration when analysing the gas kinematics of dwarf galaxy discs.
@article{2018MNRAS.476.2168M, author = {{Marasco}, A. and {Oman}, K. A. and {Navarro}, J. F. and {Frenk}, C. S. and {Oosterloo}, T.}, title = {{Bars in dark-matter-dominated dwarf galaxy discs}}, journal = {\mnras}, keywords = {ISM: kinematics and dynamics, galaxies: dwarf, galaxies: kinematics and dynamics, galaxies: structure, dark matter, Astrophysics - Astrophysics of Galaxies}, year = {2018}, month = may, volume = {476}, number = {2}, pages = {2168-2176}, doi = {10.1093/mnras/sty354}, archiveprefix = {arXiv}, eprint = {1711.09914}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2018MNRAS.476.2168M}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }
The core-cusp problem: a matter of perspective

Anna Genina, Alejandro Benı́tez-Llambay, Carlos S. Frenk, and 6 more authors

(2018) MNRAS 474 1398

Abs ADS arXiv Bib HTML PDF

The existence of two kinematically and chemically distinct stellar subpopulations in the Sculptor and Fornax dwarf galaxies offers the opportunity to constrain the density profile of their matter haloes by measuring the mass contained within the well-separated half-light radii of the two metallicity subpopulations. Walker and Peñarrubia have used this approach to argue that data for these galaxies are consistent with constant-density ‘cores’ in their inner regions and rule out ‘cuspy’ Navarro-Frenk-White (NFW) profiles with high statistical significance, particularly in the case of Sculptor. We test the validity of these claims using dwarf galaxies in the APOSTLE (A Project Of Simulating The Local Environment) Λ cold dark matter cosmological hydrodynamic simulations of analogues of the Local Group. These galaxies all have NFW dark matter density profiles and a subset of them develop two distinct metallicity subpopulations reminiscent of Sculptor and Fornax. We apply a method analogous to that of Walker and Peñarrubia to a sample of 50 simulated dwarfs and find that this procedure often leads to a statistically significant detection of a core in the profile when in reality there is a cusp. Although multiple factors contribute to these failures, the main cause is a violation of the assumption of spherical symmetry upon which the mass estimators are based. The stellar populations of the simulated dwarfs tend to be significantly elongated and, in several cases, the two metallicity populations have different asphericity and are misaligned. As a result, a wide range of slopes of the density profile are inferred depending on the angle from which the galaxy is viewed.
@article{2018MNRAS.474.1398G, author = {{Genina}, Anna and {Ben{\'\i}tez-Llambay}, Alejandro and {Frenk}, Carlos S. and {Cole}, Shaun and {Fattahi}, Azadeh and {Navarro}, Julio F. and {Oman}, Kyle A. and {Sawala}, Till and {Theuns}, Tom}, title = {{The core-cusp problem: a matter of perspective}}, journal = {\mnras}, keywords = {galaxies: dwarf, galaxies: formation, galaxies: kinematics and dynamics, dark matter, Astrophysics - Astrophysics of Galaxies}, year = {2018}, month = feb, volume = {474}, number = {1}, pages = {1398-1411}, doi = {10.1093/mnras/stx2855}, archiveprefix = {arXiv}, eprint = {1707.06303}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2018MNRAS.474.1398G}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }

2017

The low-mass end of the baryonic Tully-Fisher relation

Laura V. Sales, Julio F. Navarro, Kyle Oman, and 11 more authors

(2017) MNRAS 464 2419

Abs ADS arXiv Bib HTML PDF

The scaling of disc galaxy rotation velocity with baryonic mass (the ‘baryonic Tully-Fisher’ relation, BTF) has long confounded galaxy formation models. It is steeper than the M ∝ V³ scaling relating halo virial masses and circular velocities and its zero-point implies that galaxies comprise a very small fraction of available baryons. Such low galaxy formation efficiencies may, in principle, be explained by winds driven by evolving stars, but the tightness of the BTF relation argues against the substantial scatter expected from such a vigorous feedback mechanism. We use the APOSTLE/EAGLE simulations to show that the BTF relation is well reproduced in Λcold dark matter (CDM) simulations that match the size and number of galaxies as a function of stellar mass. In such models, galaxy rotation velocities are proportional to halo virial velocity and the steep velocity-mass dependence results from the decline in galaxy formation efficiency with decreasing halo mass needed to reconcile the CDM halo mass function with the galaxy luminosity function. The scatter in the simulated BTF is smaller than observed, even when considering all simulated galaxies and not just rotationally supported ones. The simulations predict that the BTF should become increasingly steep at the faint end, although the velocity scatter at fixed mass should remain small. Observed galaxies with rotation speeds below ∼40 km s^-1 seem to deviate from this prediction. We discuss observational biases and modelling uncertainties that may help to explain this disagreement in the context of ΛCDM models of dwarf galaxy formation.
@article{2017MNRAS.464.2419S, author = {{Sales}, Laura V. and {Navarro}, Julio F. and {Oman}, Kyle and {Fattahi}, Azadeh and {Ferrero}, Ismael and {Abadi}, Mario and {Bower}, Richard and {Crain}, Robert A. and {Frenk}, Carlos S. and {Sawala}, Till and {Schaller}, Matthieu and {Schaye}, Joop and {Theuns}, Tom and {White}, Simon D. M.}, title = {{The low-mass end of the baryonic Tully-Fisher relation}}, journal = {\mnras}, keywords = {galaxies: evolution, galaxies: haloes, galaxies: structure, Astrophysics - Astrophysics of Galaxies, Astrophysics - Cosmology and Nongalactic Astrophysics}, year = {2017}, month = jan, volume = {464}, number = {2}, pages = {2419-2428}, doi = {10.1093/mnras/stw2461}, archiveprefix = {arXiv}, eprint = {1602.02155}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2017MNRAS.464.2419S}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }

2016

Missing dark matter in dwarf galaxies?

Kyle A. Oman, Julio F. Navarro, Laura V. Sales, and 5 more authors

(2016) MNRAS 460 3610

Abs ADS arXiv Bib HTML PDF

We use cosmological hydrodynamical simulations of the APOSTLE project along with high-quality rotation curve observations to examine the fraction of baryons in ΛCDM haloes that collect into galaxies. This ‘galaxy formation efficiency’ correlates strongly and with little scatter with halo mass, dropping steadily towards dwarf galaxies. The baryonic mass of a galaxy may thus be used to place a lower limit on total halo mass and, consequently, on its asymptotic maximum circular velocity. A number of observed dwarfs seem to violate this constraint, having baryonic masses up to 10 times higher than expected from their rotation speeds, or, alternatively, rotating at only half the speed expected for their mass. Taking the data at face value, either these systems have formed galaxies with extraordinary efficiency - highly unlikely given their shallow potential wells - or their dark matter content is much lower than expected from ΛCDM haloes. This ‘missing dark matter’ is reminiscent of the inner mass deficit of galaxies with slowly rising rotation curves, but cannot be explained away by star formation-induced ‘cores’ in the dark mass profile, since the anomalous deficit applies to regions larger than the luminous galaxies themselves. We argue that explaining the structure of these galaxies would require either substantial modification of the standard ΛCDM paradigm or else significant revision to the uncertainties in their inferred mass profiles, which should be much larger than reported. Systematic errors in inclination may provide a simple resolution to what would otherwise be a rather intractable problem for the current paradigm.
@article{2016MNRAS.460.3610O, author = {{Oman}, Kyle A. and {Navarro}, Julio F. and {Sales}, Laura V. and {Fattahi}, Azadeh and {Frenk}, Carlos S. and {Sawala}, Till and {Schaller}, Matthieu and {White}, Simon D. M.}, title = {{Missing dark matter in dwarf galaxies?}}, journal = {\mnras}, keywords = {galaxies: haloes, galaxies: structure, dark matter, Astrophysics - Astrophysics of Galaxies, Astrophysics - Cosmology and Nongalactic Astrophysics}, year = {2016}, month = aug, volume = {460}, number = {4}, pages = {3610-3623}, doi = {10.1093/mnras/stw1251}, archiveprefix = {arXiv}, eprint = {1601.01026}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2016MNRAS.460.3610O}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }
The APOSTLE simulations: solutions to the Local Group’s cosmic puzzles

Till Sawala, Carlos S. Frenk, Azadeh Fattahi, and 13 more authors

(2016) MNRAS 457 1931

Abs ADS arXiv Bib HTML PDF

The Local Group galaxies offer some of the most discriminating tests of models of cosmic structure formation. For example, observations of the Milky Way (MW) and Andromeda satellite populations appear to be in disagreement with N-body simulations of the ‘lambda cold dark matter’ (ΛCDM) model: there are far fewer satellite galaxies than substructures in CDM haloes (the ‘missing satellites’ problem); dwarf galaxies seem to avoid the most massive substructures (the ‘too-big-to-fail’ problem); and the brightest satellites appear to orbit their host galaxies on a thin plane (the ‘planes of satellites’ problem). Here we present results from APOSTLE (A Project Of Simulating The Local Environment), a suite of cosmological hydrodynamic simulations of 12 volumes selected to match the kinematics of the Local Group (LG) members. Applying the EAGLE code to the LG environment, we find that our simulations match the observed abundance of LG galaxies, including the satellite galaxies of the MW and Andromeda. Due to changes to the structure of haloes and the evolution in the LG environment, the simulations reproduce the observed relation between stellar mass and velocity dispersion of individual dwarf spheroidal galaxies without necessitating the formation of cores in their dark matter profiles. Satellite systems form with a range of spatial anisotropies, including one similar to the MWs, confirming that such a configuration is not unexpected in ΛCDM. Finally, based on the observed velocity dispersion, size, and stellar mass, we provide estimates of the maximum circular velocity for the haloes of nine MW dwarf spheroidals.
@article{2016MNRAS.457.1931S, author = {{Sawala}, Till and {Frenk}, Carlos S. and {Fattahi}, Azadeh and {Navarro}, Julio F. and {Bower}, Richard G. and {Crain}, Robert A. and {Dalla Vecchia}, Claudio and {Furlong}, Michelle and {Helly}, John. C. and {Jenkins}, Adrian and {Oman}, Kyle A. and {Schaller}, Matthieu and {Schaye}, Joop and {Theuns}, Tom and {Trayford}, James and {White}, Simon D. M.}, title = {{The APOSTLE simulations: solutions to the Local Group's cosmic puzzles}}, journal = {\mnras}, keywords = {galaxies: evolution, galaxies: formation, cosmology: theory, Astrophysics - Astrophysics of Galaxies, Astrophysics - Cosmology and Nongalactic Astrophysics}, year = {2016}, month = apr, volume = {457}, number = {2}, pages = {1931-1943}, doi = {10.1093/mnras/stw145}, archiveprefix = {arXiv}, eprint = {1511.01098}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2016MNRAS.457.1931S}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }

2015

The unexpected diversity of dwarf galaxy rotation curves

Kyle A. Oman, Julio F. Navarro, Azadeh Fattahi, and 9 more authors

(2015) MNRAS 452 3650

Abs ADS arXiv Bib HTML PDF

We examine the circular velocity profiles of galaxies in Λ cold dark matter (CDM) cosmological hydrodynamical simulations from the EAGLE and LOCAL GROUPS projects and compare them with a compilation of observed rotation curves of galaxies spanning a wide range in mass. The shape of the circular velocity profiles of simulated galaxies varies systematically as a function of galaxy mass, but shows remarkably little variation at fixed maximum circular velocity. This is especially true for low-mass dark-matter-dominated systems, reflecting the expected similarity of the underlying CDM haloes. This is at odds with observed dwarf galaxies, which show a large diversity of rotation curve shapes, even at fixed maximum rotation speed. Some dwarfs have rotation curves that agree well with simulations, others do not. The latter are systems where the inferred mass enclosed in the inner regions is much lower than expected for CDM haloes and include many galaxies where previous work claims the presence of a constant density ‘core’. The ‘cusp versus core’ issue is thus better characterized as an ‘inner mass deficit’ problem than as a density slope mismatch. For several galaxies, the magnitude of this inner mass deficit is well in excess of that reported in recent simulations where cores result from baryon-induced fluctuations in the gravitational potential. We conclude that one or more of the following statements must be true: (i) the dark matter is more complex than envisaged by any current model; (ii) current simulations fail to reproduce the diversity in the effects of baryons on the inner regions of dwarf galaxies; and/or (iii) the mass profiles of ‘inner mass deficit’ galaxies inferred from kinematic data are incorrect.
@article{2015MNRAS.452.3650O, author = {{Oman}, Kyle A. and {Navarro}, Julio F. and {Fattahi}, Azadeh and {Frenk}, Carlos S. and {Sawala}, Till and {White}, Simon D. M. and {Bower}, Richard and {Crain}, Robert A. and {Furlong}, Michelle and {Schaller}, Matthieu and {Schaye}, Joop and {Theuns}, Tom}, title = {{The unexpected diversity of dwarf galaxy rotation curves}}, journal = {\mnras}, keywords = {galaxies: haloes, galaxies: structure, dark matter, Astrophysics - Astrophysics of Galaxies, Astrophysics - Cosmology and Nongalactic Astrophysics}, year = {2015}, month = oct, volume = {452}, number = {4}, pages = {3650-3665}, doi = {10.1093/mnras/stv1504}, archiveprefix = {arXiv}, eprint = {1504.01437}, primaryclass = {astro-ph.GA}, adsurl = {https://ui.adsabs.harvard.edu/abs/2015MNRAS.452.3650O}, adsnote = {Provided by the SAO/NASA Astrophysics Data System}, }

Contents